Підтримай сайт
Diagram "moment curvature"
| Step | Moment, kNm | Curvature, 1/r | Tension in s1, MPa | Tension in s2, MPa |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 116 | 0.00126 | 60 | -89 |
| 2 | 161 | 0.00183 | 91 | -124 |
| 3 | 201 | 0.00237 | 123 | -156 |
| 4 | 234 | 0.00288 | 155 | -184 |
| 5 | 264 | 0.00336 | 187 | -209 |
| 6 | 289 | 0.00471 | 228 | -228 |
| 7 | 290 | 0.00625 | 228 | -228 |
| 8 | 291 | 0.00777 | 228 | -228 |
| 9 | 290 | 0.00924 | 228 | -228 |
| 10 | 286 | 0.01179 | 228 | -228 |
Explanation to the calculation
Відповідно до п.3.1.5[1] та п.4.2[2], несуча здатність залізобетонного елементу прямокутного перерізу на дію згинального моменту визначена за формулами (4.3)[2] та (4.4)[2].
Система двох нелінійних алгебраїчних рівнянь(4.3 - 4.4) з двома невідомими розв’язуються підбором з контролем критеріїв вичерпання несучої здатності на кожному кроці розрахунків. Для оцінки напружено-деформованого стану розрахункового перерізу використовується деформаційний метод, алгоритм розв’язання задачі згідно деформаційного методу наведений в Додатку А[2].
За результатами рішення систем рівнянь (4.3 - 4.4) будується діаграма «момент – кривизна». Найбільша величина зафіксована на цій діаграмі і приймаються за несучу здатність. В разі, якщо визначена величина несучої здатності будє меншою за зовнішні впливи необхідно виконати зміну розмірів перерізу, армування або міцності бетону.
Boundary conditions
Максимальна ширина перерізу з/б елементу b = 1 м, мінімальна - 0.05 м;
Максимальна висота перерізу з/б елементу h = 2.5 м, мінімальна - 0.05 м;
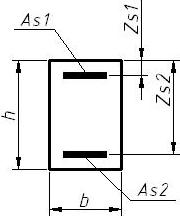
Відстань 1-го стрижня або прошарку арматури від найбільш стиснутої грані перерізу Zs1 > 0;
Відстань 2-го стрижня або прошарку арматури від найбільш стиснутої грані перерізу Zs2 > Zs1, Zs2 < h;
Максимальна площа арматури As1 і As2 = 0.005 м2, мінімальна - 0.05%.
References
1. ДБН B.2.6-98 "Бетонні та залізобетонні конструкції".
2. ДСТУ Б В.2.6-156:2010 "Бетонні та залізобетонні конструкції з важкого бетону. Правила проектування".