Спрощений метод розрахунку з/б елементу таврового перерізу з одиничним армуванням

Розрахунок залізобетонного таврового перерізу на згин з одиничним армуванням за спрощеною методикою. Приклад розрахунку

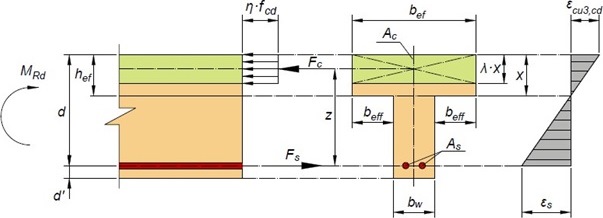
Сьогодні розберемо виведення основних формул для підбору арматури залізобетонного таврового перерізу з одиничним армуванням, в якого висота стиснутої зони знаходиться в межах полиці, λ · x ≤ h_ef, або нейтральна вісь проходить в межах полиці, а не ребра. Назвемо його випадок – а. Такий алгоритм дуже схожий на алгоритм прямокутного перерізу з одичним армуванням.
Складаємо рівняння суми всіх сил, як ми це робили в попередній раз:

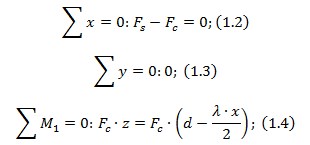
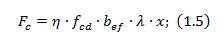
Отже несуча здатність залізобетонного таврового перерізу з одиничним армуванням

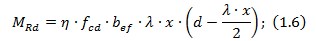
З виразу вище записуємо квадратне рівняння

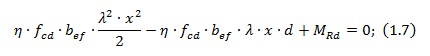
З квадратного рівняння знаходимо висоту стиснутої зони за формулою

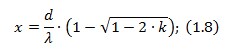
λ - коефіцієнт, що визначає розрахункову висоту стиснутої зони бетону п.3.1.6.2 норм [1]
Звідки невідомий коефіцієнт з формули вище визначається за формулою

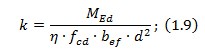
f_cd - розрахункове значення міцності бетону на стиск,табл.3.1 норм [1];
η - коефіцієнт,що визначає різний вплив факторів на міцність бетону п.3.1.6.2 норм [1]

Як ви замітили, тут все аналогічно прямокутному перерізу з одиничним армуванням, тільки замість ширини перерізу b ми використовуємо ширину полиці b_ef таврового перерізу.

Момент що може сприйняти полиця таврового перерізу, якщо вважати що λ · x = h_ef

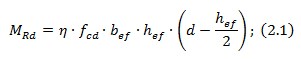
Необхідну площу розтягнутої робочої арматури можна визначити за формулою

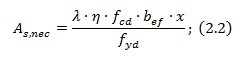
Також можна визначити за формулою

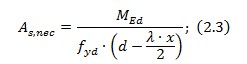
f_yd - розрахункове значення міцності арматури на розтяг,п.3.2.1.4 норм [2];
Цей алгоритм діє при умові якщо фактична висота стиснутої зони не перевищує висоти полиці та граничної висоти стиснутої зони

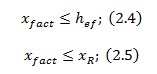
Але тут зрозуміло, що якщо виконується перша умова, то відповідно і виконується друга.

Фактична висота стиснутої зони визначається за формулою

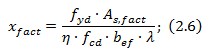
Граничне значення висоти стиснутої зони можна визначити за формулою

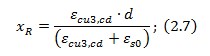
ε_(cu3,cd) - розрахункова гранична деформація стиску бетону,згідно табл.3.1 норм [1];
ε_s0 - відносна деформація видовження арматури,згідно формули 3.16 норм [2];

Приклад розрахунку залізобетонного таврового перерізу на згин з одиничним армуванням, в якого нейтральна вісь проходить в межах полиці

Вихідні дані:

M_Ed = 5000 кНсм - зовнішній розрахунковий згинальний момент;
h_ef = 15 см - висота полиці таврового перерізу;
b_ef = 30 см - ширина полиці таврового перерізу;
b_w = 15 см - ширина нижнього ребра таврового перерізу;
h = 30 см - висота прямокутного перерізу;
d = 27 см - робоча (ефективна) висота перерізу;
η = 1 - п.3.1.6.2 норм [2];
λ = 0,8 - п.3.1.6.2 норм [2];
f_cd = 14,5 МПа - табл.3.1 норм [1];


ε_(cu3,cd) = 3,1 проміле - табл.3.1 норм [1];
E_s =2 10000 МПа - табл.3.4 норм [2];
f_(cm,cube) = 32 МПа - табл.3.1 норм [1];

Момент що може сприйняти полиця таврового перерізу, якщо вважати що ? · x = h_ef

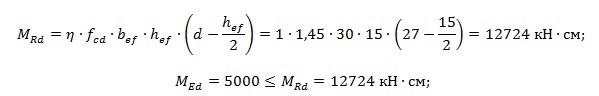
Отже нейтральна вісь проходить в межах полиці.
Визначаємо коефіцієнт

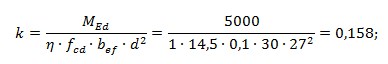
Висота стиснутої зони бетону

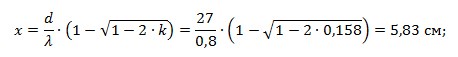
Відносна деформація видовження арматури

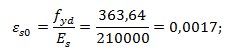
Гранична висота стиснутої зони бетону

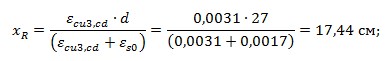
Перевірка умови

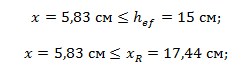
Умова виконується, отже йдемо далі.
Необхідна площа розтягнутої арматури

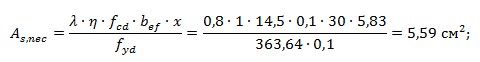
Згідно сортаменту арматурної сталі, підбираємо два стержні діаметром 20 мм з фактичною площею поперечного перерізу

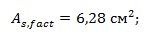
Фактична висота стиснутої зони

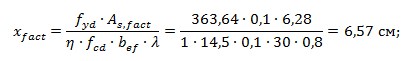
Визначаємо несучу здатність залізобетонного прямокутного перерізу та перевіряємо умову

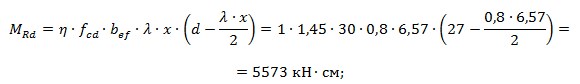
Перевірка умови

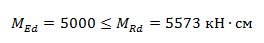
Умова виконується отже несуча здатність таврового перерізу на дію згинального моменту забезпечена

Перелік посилань

1. ДБН B.2.6-98 "Бетонні та залізобетонні конструкції".
2. ДСТУ Б В.2.6-156:2010 "Бетонні та залізобетонні конструкції з важкого бетону. Правила проектування".

Автор статті
Юрій Воробець